This paper makes several contributions about optimization :

  • They prove that Heavy Ball (HB) or Nesterov methods are not optimals and can be worse than SGD.
  • In practice, HB takes advantage of the mini-batching used in training.
  • They designed a new optimizer Accelerated Stochastic Gradient Descent (ASGD) which has a faster convergence rate.

See Section 2 for notations.

Accelerated SGD

Here, \(\kappa = \frac{\lambda_1(H)}{\lambda_d(H)}\) with H equals to the Hessian matrix of \(f\), the function to optimize. It’s called the condition number or the long step parameter. In practice, it’s estimated and is intended to give an estimate of the ratio of the largest and smallest curvatures of the function; for convex functions, this is just the condition number. \(\xi\) characterize the trade-off between the stochastic condition number and the exact condition number.

Convergence

In Corollary 1 and 2, the authors show that ASGD has a faster convergence rate than SGD by a factor of \(\sqrt{\kappa}\)

The authors show that HB methods do not have an upper-bound and requires \(\Omega (\kappa log \frac{1}{\epsilon})\) iterations to converge. In comparison, ASGD requires \(O (\sqrt{\kappa} \quad log \kappa \quad log \frac{1}{\epsilon})\).

Experiments

Using a Resnet-50, the authors test on CIFAR-10.

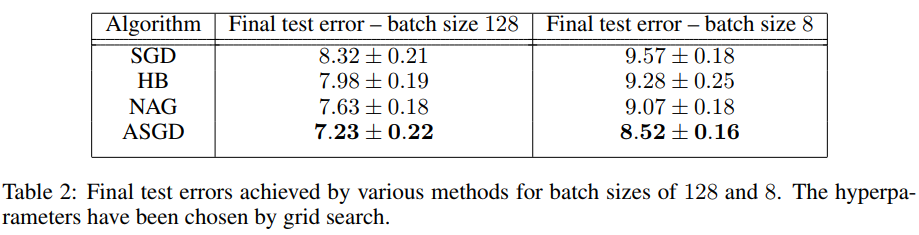
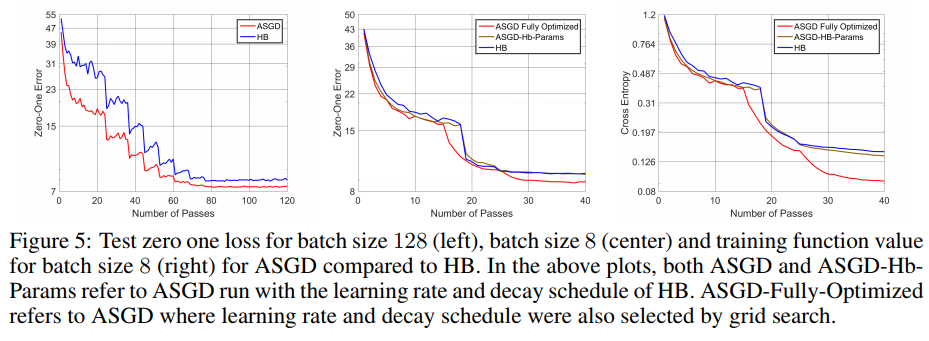
NOTE When trained with a batch size of 128, the model has been training for 120 epochs versus 40 epochs for batch size 8.

Take home message : HB and NAG are not optimals, they are good because of mini-batching.

Pytorch code : https://github.com/rahulkidambi/AccSGD

NOTE the discussion on OpenReview is quite interesting.