The authors propose a novel layer to perform non-linear transformations inside a neural network. They design a Vector Field Layer which learns a vector field to be applied to the input.

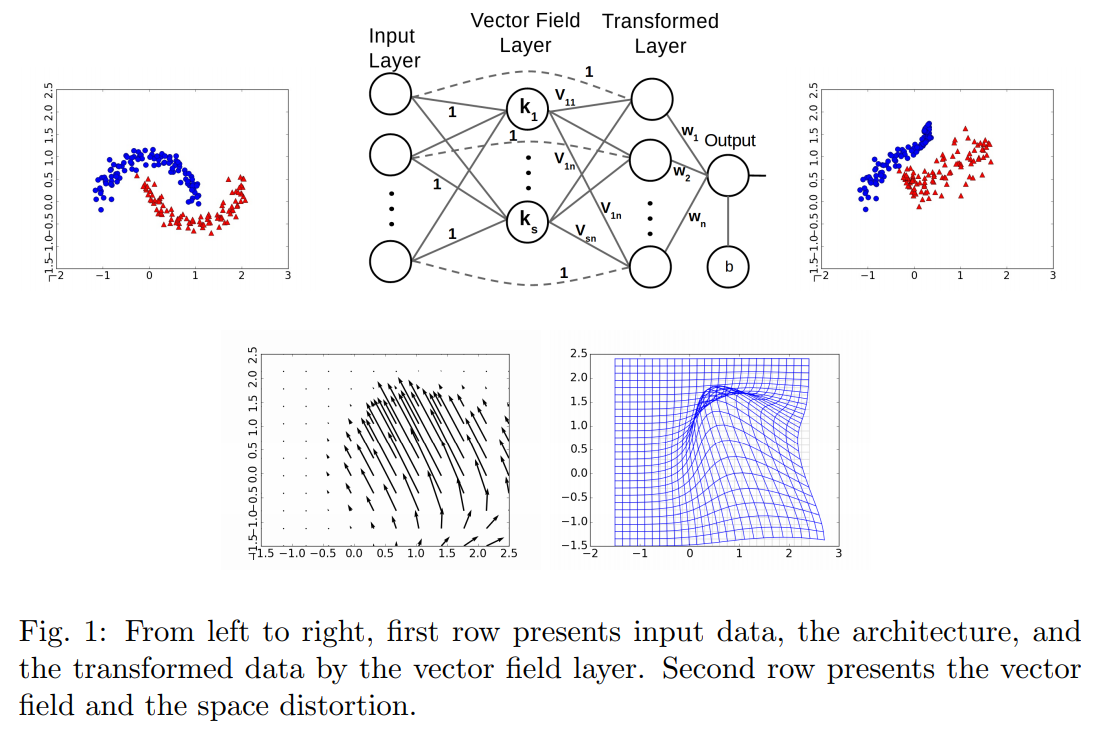
Let \(X\) be the input, \(\mu_{i}\) the means of the \(S\) gaussians and \(V_{i}\) the \(S\) learned vectors.

We can compute \(X_{i+1} = X_{i} + h(K(X_{i}, \theta))\), the transformed input.

\(h\) is the step-size, \(\theta\) are the parameters \((\mu_{i}, V_{i})\)

\(K(X_{i}, \theta)\) is a weighted sum of vectors, the weights are a result of a kernel function. (see eq. 2-3).

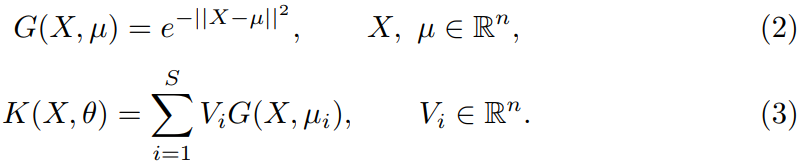
While this is early work, it’s a really interesting method.