Bayesian Image Quality Transfer (IQT) with CNNs

The goal is to upsample low-resolution (LR) dMRI images to high resolution (HR) and measure uncertainty in the prediction.

Highlights

  • Previous models were limited to 2D images, but the proposed model works on 3D volumes and outperforms others in accuracy and speed (whole-brain DTI SR in 1s).

  • Ability to estimate uncertainty in the SR mapping.

Summary

Model

The super-resolution (SR) task is a patch-wise regression from LR to HR. The authors use a baseline 2D CNN (Efficient subpixel-shifted convolutional network, CVPR 2016) and extend it to 3D volumes (3D-ESPCN).

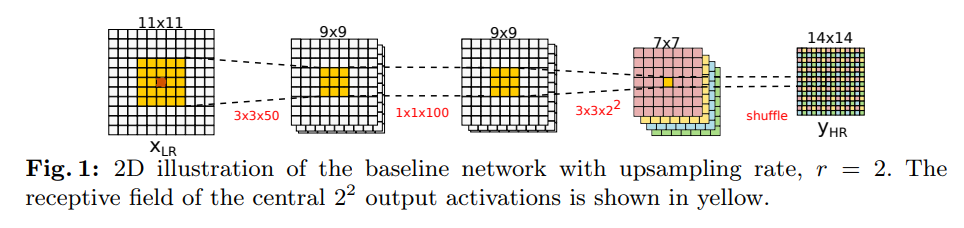
NOTE: Instead of upsampling a LR image and refining it thorugh the CNN, the LR image is directly processed and the last feature maps are combined to produce a HR image (learned interpolation).

Computational cost is reduced and there no loss of information from upsampling the LR image before processing

A receptive field of 5x5x5 is used to predict 1x1x1 feature maps (resulting in a 2x2x2 HR patch in the final image after shuffling).

The network is in theory trained using L2 reconstruction.

Uncertainty estimation

The authors address 2 types of uncertainty:

  • Intrinsic uncertainty (variance of the statistical mapping from LR to HR, aka one-to-many problem; independent of the amount of training data)
  • Parameter uncertainty (ambiguity in model parameters)

Intrinsic uncertainty

Minimizing a mean squared error is equivalent to minimising the NLL under a Gaussian noise model:

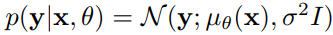
In this case, the variance is fixed and represents the intrinsic uncertainty in the mapping. In practice however, uncertainty is not constant across all spatial locations and image channels. The authors address this issue by using a heteroscedastic noise model to estimate the variation across the image. The likelihood becomes:

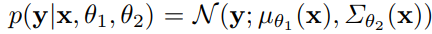
Here, the mean and variance are estimated by two different 3D-ESPCN models:

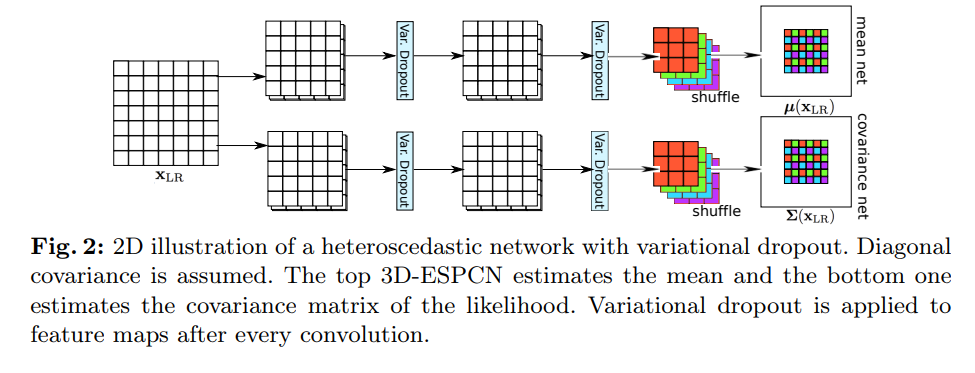
Parameter uncertainty

Instead of relying in a single estimate of the network parameters, the authors propose to limit overfitting using a bayesian approach with Variational Dropout. In summary, Gaussian noise is injected in the network weights during training, but the amount of noise is learned.

Experiments

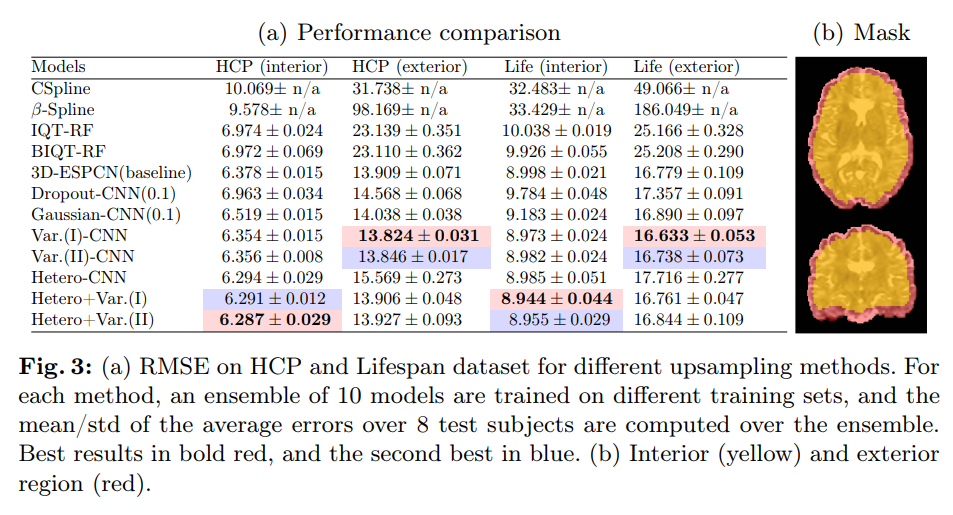
Super resolution

  • Human Connectome project (multiple sets of 8 subjects, HR + downsampled LR)
  • Lifespan dataset (different acquisition than HCP, lower resolution, different age range)

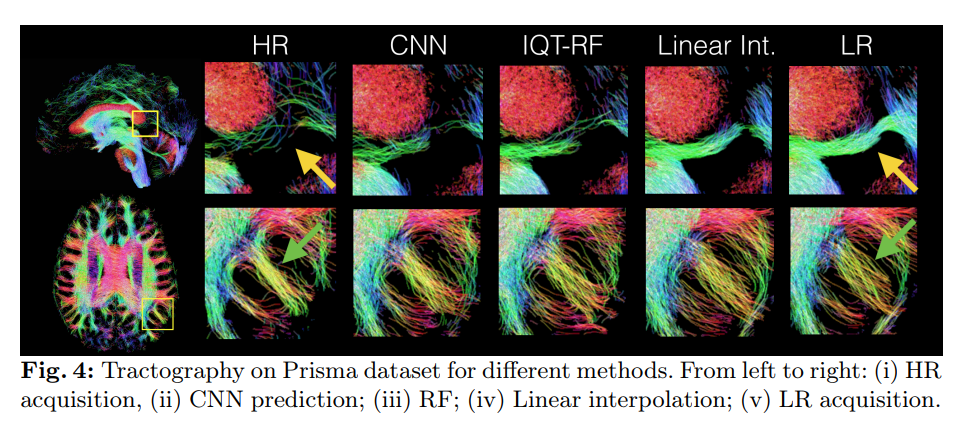
Tractography with SR

  • Prisma dataset (3T scanner, similar to HCP)

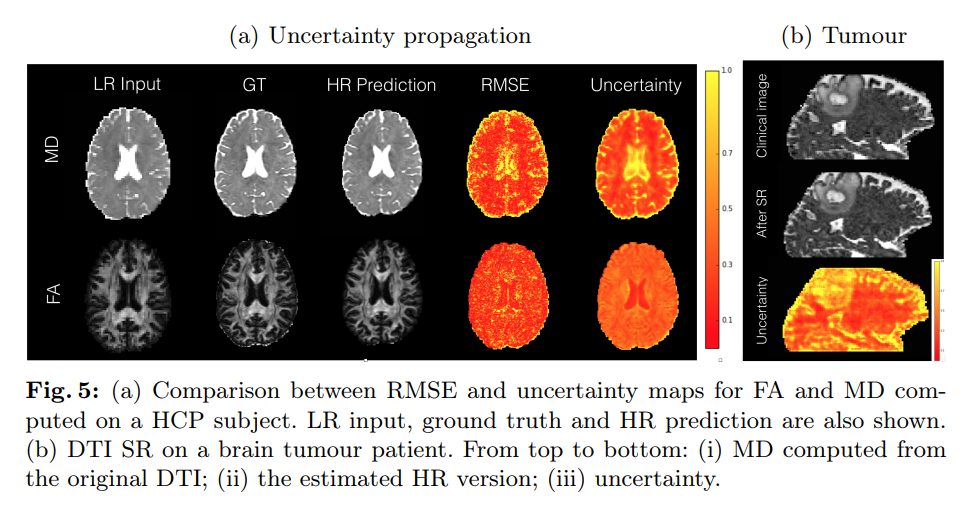
Uncertainty visualization