Rotate your Networks: Better Weight Consolidation and Less Catastrophic Forgetting
This paper is built upon Elastic Weight Consolidation 1 (EWC), a common method to avoid catastrophic forgetting. In this setting, we want to learn the \(Kth\) task without forgetting the \(K-1\) previous tasks. To do so, EWC compute the optimal \(\theta_{:K}\) given \(\theta_{:K-1}\) such that it maximizes the posterior \(p_{:K} = p(\theta \vert D_{:K})\) where \(D_{:K}\) are all datasets up to task \(K\).
This can be done using the Fisher matrix of previous task \(\bar F_{:K-1}\) (See eq. 3).
An assumption that EWC requires is that the Fisher matrix must be block diagonal, which is hard to get in practice.
This paper aims to approximate a block diagonal Fisher matrix by doing a reparameterization of all weights in the network. I’ll only describe the process for the fully-connected layer, but the process is similar for CNNs.
Using eq. 7, we can approximate the Fisher matrix from two components which are available : the inputs and the gradients.
From those two components, we can find two new weights \(U_{1}, U_{2}\). These weights will provide an approximate diagonalisation of \(W\), thus preventing catastrophic forgetting. The learnable weight then become \(W' = U^{T}_{2}WU^{T}_{1}\).
Results
On multiple datasets, the authors show that their method works better than standard EWC.
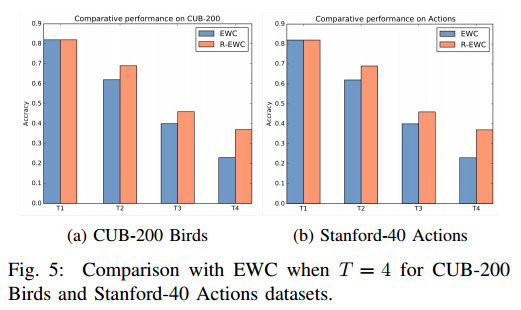
-
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Desjardins, G., Rusu, A. A., … & Hassabis, D. (2017). Overcoming catastrophic forgetting in neural networks. Proceedings of the National Academy of Sciences, 114(13), 3521-3526. ↩