NOTE : This paper is more of a review of the current state of clustering using deep learning. So do not expect flashy results.

The authors decompose their problem in 4 sections :

  • The architecture
  • The number of features to use (1 layer versus multiple)
  • The non-clustering loss
  • The clustering loss

The first 3 are straigthfoward, it seems that everyone uses a CNN autoencoder.

The last one is interesting because it forces the network to learn features that would be easy to clusters. Given a set of K centers \(\mu\), a batch of N samples \(z\) and an association matrix \(s\), we define the k-means loss as :

\[L(\theta)=\sum^{N,K}_{i=1,k=1}s_{i,k} \Vert z_{i}-\mu_{k}\Vert^2\]

Soft assignments

The previous equation has a major issue, it requires hard assignments. The authors show how to compute soft assignments. The authors define \(q_{ij}\) the similarity between a point \(i\) and a cluster \(j\). All points are then made stricter by creationg a distribution P :

\[p_{ij} = \frac{\frac{q^2_{ij}}{\sum_{i'}q_{i'j}}}{\sum_{j'}(\frac{q^2_{ij'}}{\sum_{i'}q_{i'j'}})}\]

The added loss is the KL divergence between P and Q. This loss forces the network to compute assignments with confidence. The authors also argue that this loss prevent large clusters from distorting the hidden feature space.

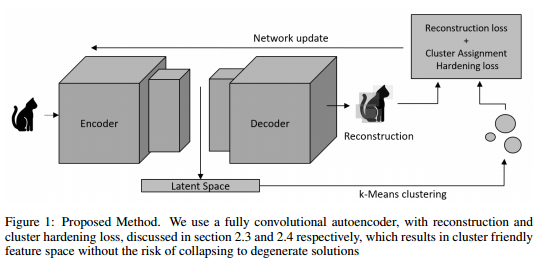
The authors use a two-step training regime. They first train the autoencoder without the clustering loss and then add it.

The authors show a t-sne plot of their embedding which seems superior to the autoencoder alone.

They also test with COIL20 which is a dataset similar to CIFAR10 but with less samples and 20 classes.

CODE : Theano