Matching Networks for One Shot Learning
Description
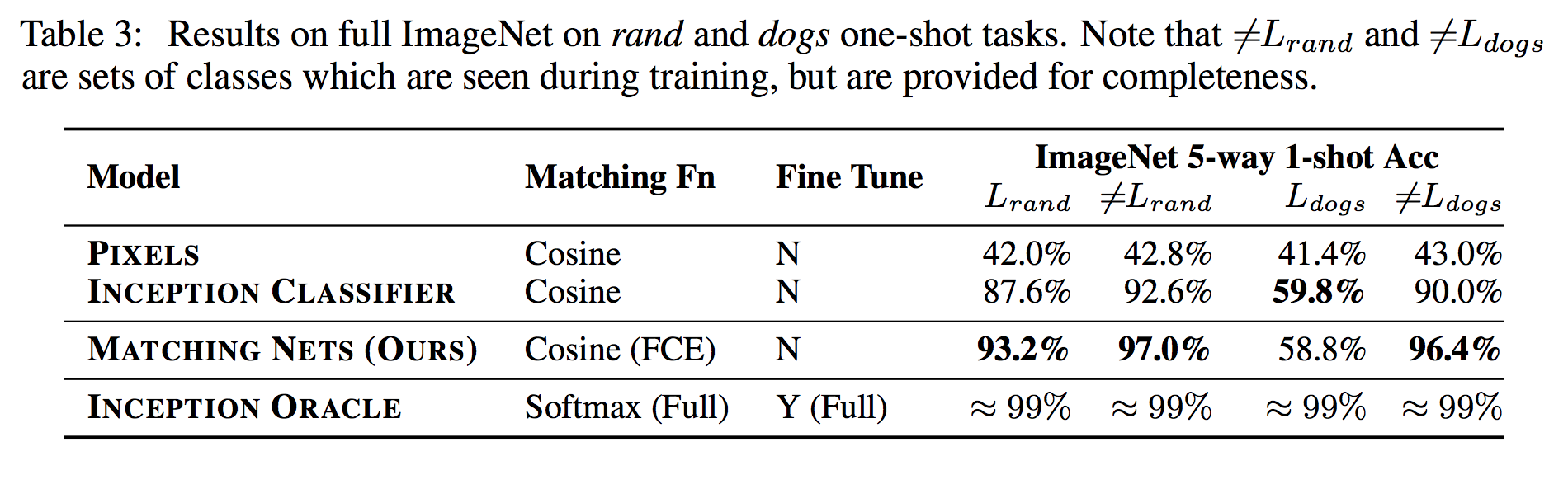
This paper proposes a solution for small data sets which suffer from overfitting. The authors employ a metric learning which helps the network to rapidly learn from small data set. They applied this idea on a small set of Image Net and they improve an accuracy from 87.6% to 93.2%.
They use the advantages of one shot learning, but for prediction on the target, they investigate a metric to find how much an unseen sample is simmilar to set of seen samples in a episod and this similarity can be present as a weight on classes. This metric plays the same role as attention or a kernel function. The authors used a cosine distance on two vectors as a metric.
Suppose \((x_{i},y_{i})\) is a given (input, class) and \(\bar{x}\) is a given input and predicted label \(\bar{y}\) calculated as:
\[\bar{y} = \sum_{i=1}^k a(\bar{x},x_i) y_{i}\]A small support set contains of \(k\) label example with input \(x\) and lable \(y\), \(S= {(x_{i},y_{i})}_{i=1}^k\), given a new example \(\bar{x}\), we want to know the probability that it is an example of a given class \(P(\bar{y}\mid\bar{x},S)\) where \(P\) is parametrized by a neural network. Therefore \(S\) maps to a classifier \(c_{s}(\bar{x})\). Simply, suppose a task \(T\) has a distribution over lable sets \(L\).
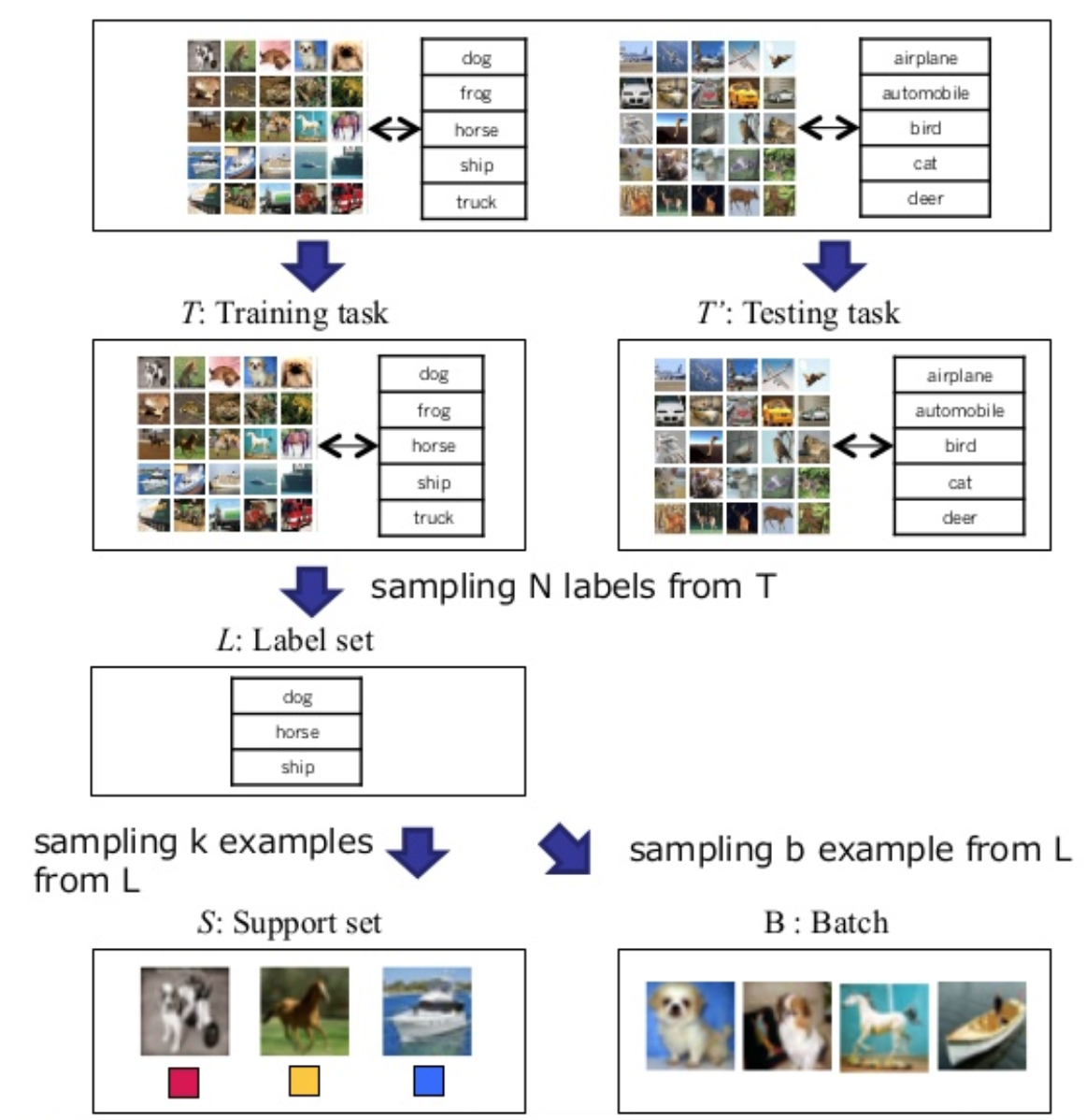
First a set \(L\) from task \(T\) is sampled, Then from these sample labels, the support set \(S\) and a batch \(B\) are sampled. The Maching network has to minimize the prediction of lables in batch \(B\) conditioned on support set \((S)\).
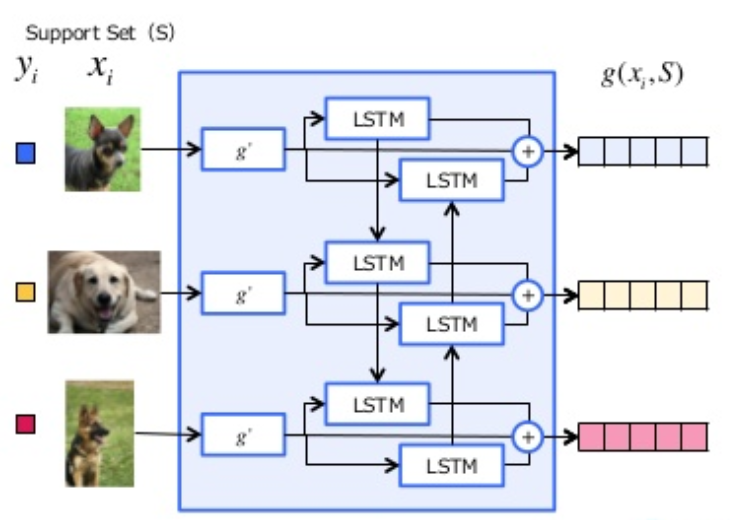
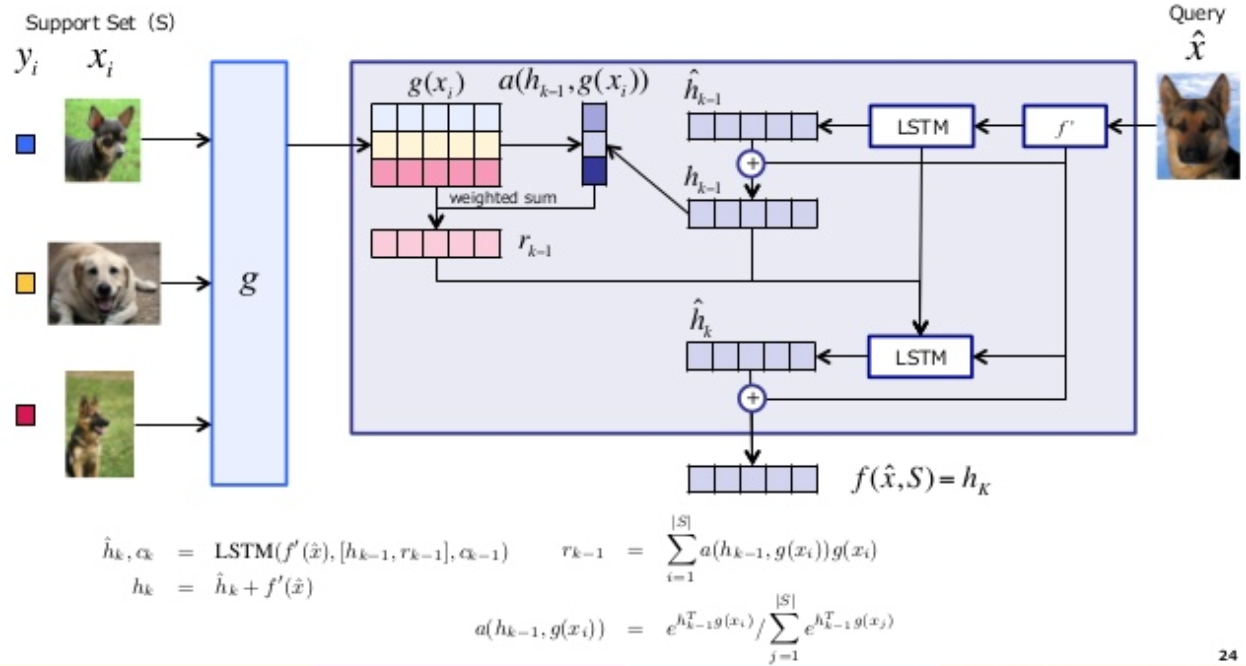
For a similarity metric, two embeding functions \(f\) and \(g\) need to take similarity on feature space X. function \(g\) has embeded \(x_{i}\) independently from other elements but \(S\) could be able to effect how be embeded \(\bar{x}\) through function \(f\). Then an attention kernel calculate cosin distance on these functions (similar to nearest neighbor).
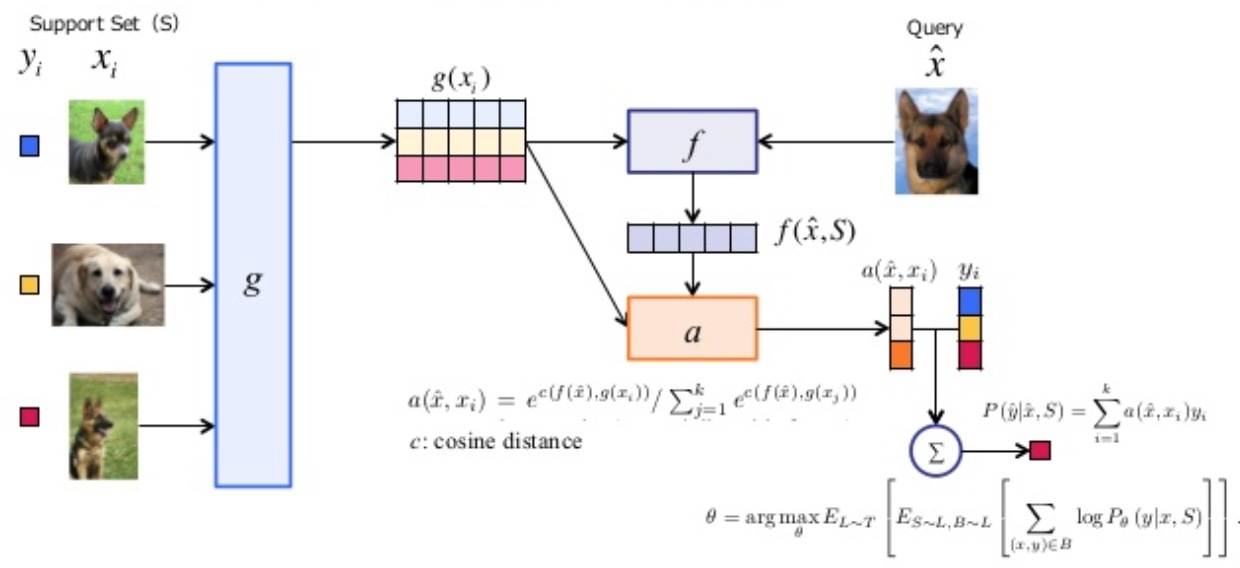
The embeding of \(x_{i}\) is a neural network (VGG) follow by a Bi-LSTM. The function f is a neural network (VGG) and then the embeding function g applied to each element \(x_{i}\) to process the kernel for each set of S. Note that \(\bar{y}\) is a linear combination of the lables in support set.
Results