Dynamic Routing Between Capsules
Summary
A capsule is a group of neurons processing vectors as input, and computing a vector as output. The length of the output vector represents the probability that an “entity” exists (an object, object part, or any other abstract concept), and its orientation represents the instantiation parameters of the “entity”.
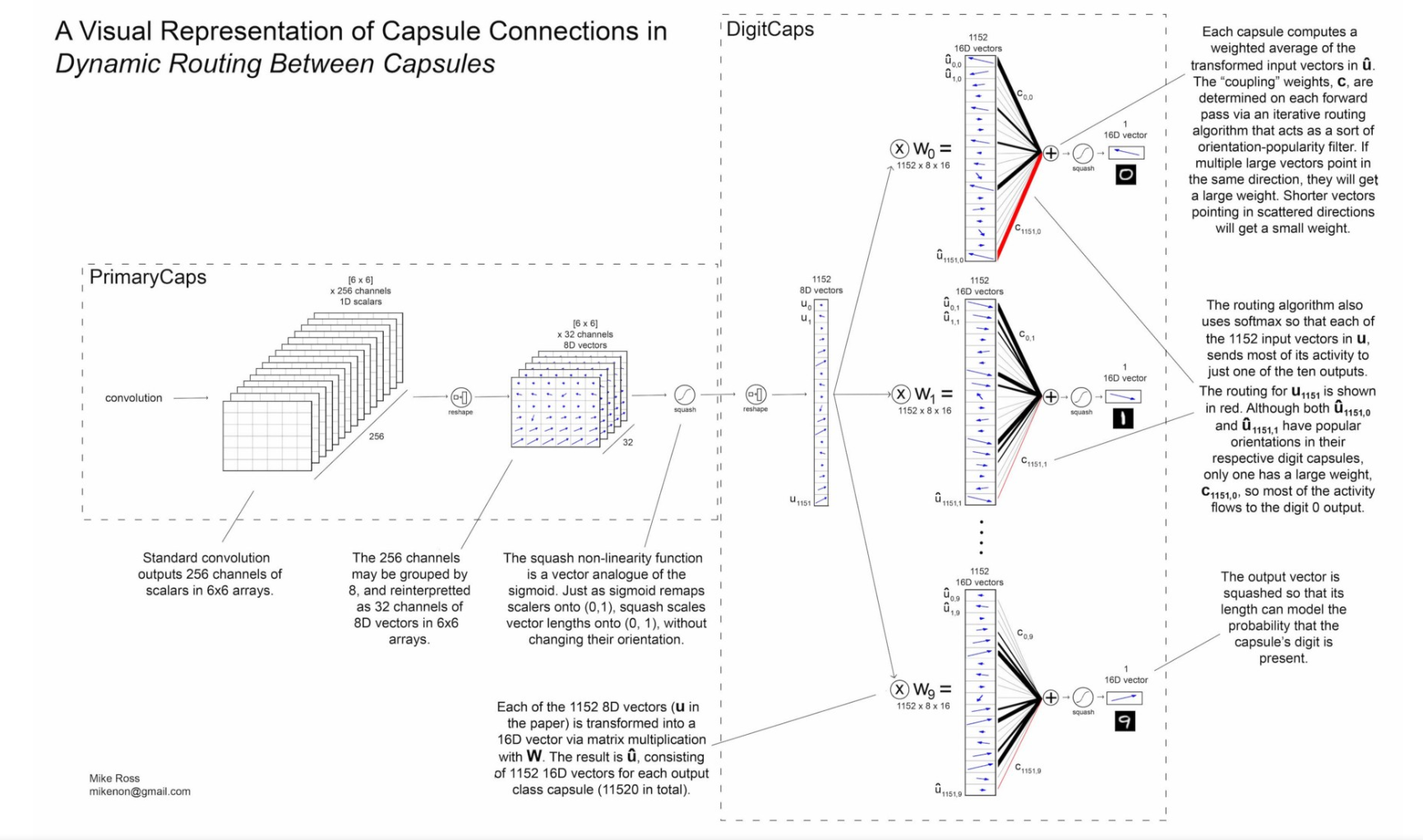
Basically, instead of processing layers of scalar values, the capsule network processes layers of vectors. A new non-linear “squashing” activation function is introduced, analogous to the sigmoid but for vector outputs (short vectors are shrunk near zero, and long vectors are shrunk just under unit length).
Squashing function: 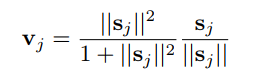

The coupling coefficients \(c_{ij}\) sum to one and computed by a “routing softmax”, using as initial logits the log prior probabilities that capsule i should be coupled to capsule j. The log priors can be learned at the same time as the rest of the network, but do not depend on the input image; they depend only on the location and type of the two capsules. The coefficients are iteratively refined by measuring the “agreement” between the output \(v_j\) of a capsule in the layer above and the prediction vector made by capsule \(i\). This agreement is simply the scalar product between the two vectors and is added to the initial logits.
The convolutional version of the capsule network simply uses “grids” of vectors as layers.

In the MNIST case, a multiclass loss is used for each digit \(k\), with the caveat that a digit class cannot be present more than once.
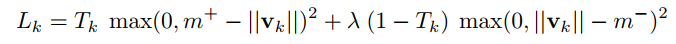
In this loss, \(T_k = 1\) if and only if a digit of class \(k\) is present in the image, \(m^+ = 0.9\) and \(m^- = 0.1\).
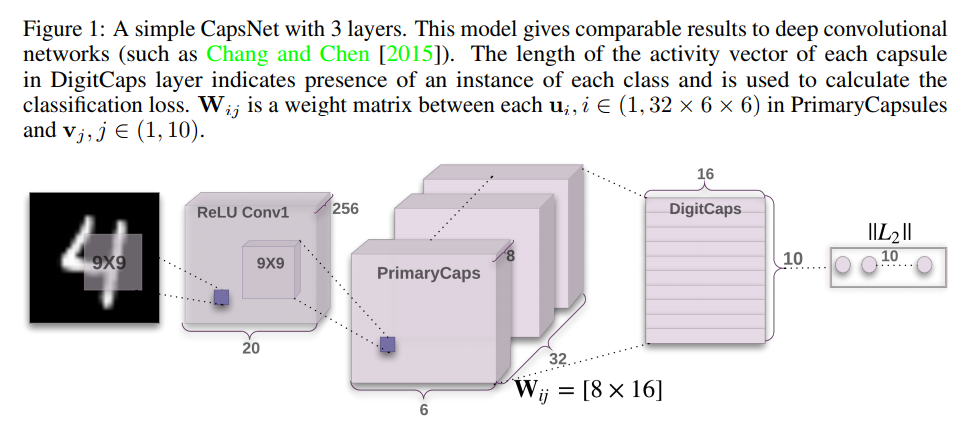
Original Capsule Network figure from paper:
Supplementary figure provided for comprehension:
As a regularization method, the DigitCaps layer representation is also used to reconstruct images of a given class (by adding a 3-layer decoder):
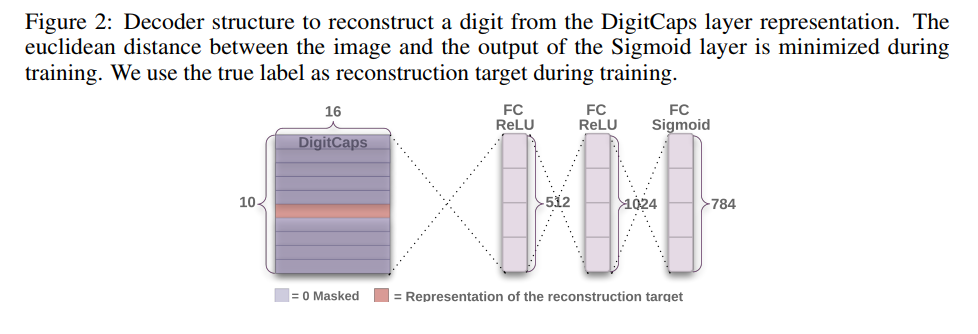
Results

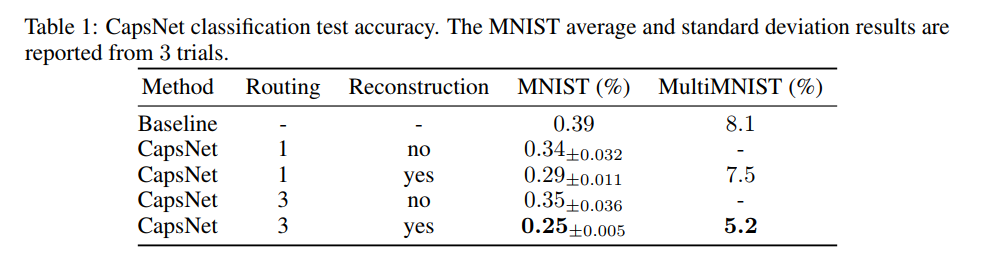
Test results on MNIST:
Note: The baseline is a standard 3-layer CNN [conv-256,conv-256,conv-128, fc-328, fc-192], with 5x5 kernels and stride 1.
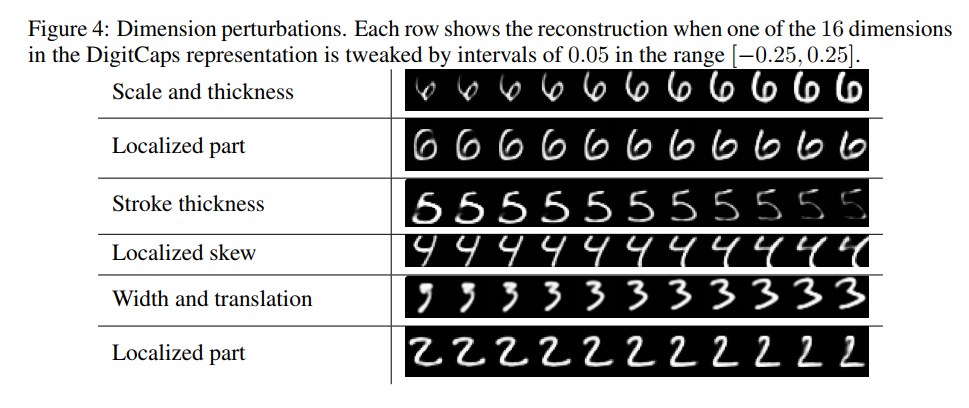
Results on MultiMNIST:
