Description

In this paper, they want to increase the spatial resolution of hyperspectral images to match with the different spacial resolution of the different imaging sensor technologies. For that they created a three-dimensional full CNN (3D-FCNN) to perform super resolution of hyperspectral images.

To do that they exploit both the spatial context of neighboring pixels and spectral correlation of neighboring bands. Changing the 2D convolution to a 3D convolution.

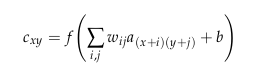
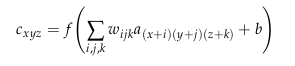
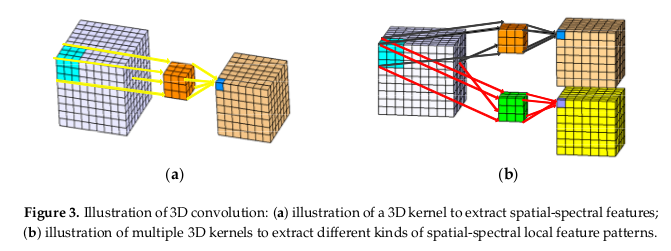
The architecture of the proposed 3D-FCNN fully explores spatial-spectral features in the data cube. First, because of the low resolution of the input, they upscale the input of the desired output size using a bicubic interpolation. This step alleviates the spectral distortion during the 3D convolution. In the structure, we find four convolutional layers and the input image will be \(33 \times 33 \times c \times 1\), where \(33 \times 33\) is the spatial dimension, \(c\) the number of spectral layers and the \(1\) is the color channel for the HSI (Hyperspectral imaging). Between those four, the ‘ReLU’ function is used as activation function for nonlinear mapping.

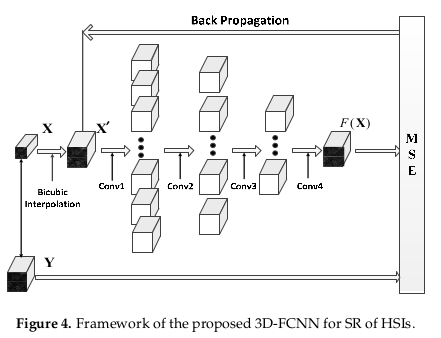
In the table below, we have the size of the different kernel associated with layers.

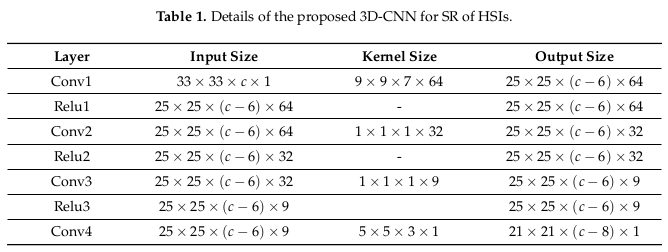
To provide border effects they don’t add any padding in any convolutions. At the end the cost function, is the MSE (mean squared error) between outputs and ground-truth.

Train with good parameters they want to use this trained network on different datasets obtained from the same sensor.

Results

In this paper, they use the mean peak signal-to-noise ratio (MPSNR) and the mean structural similarity (MSSIM) to evaluate the spatial performance of the system. To provide a score on the spectral performance they used spectral angle mapper (SAM) between the reconstructed spectra and their corresponding ground-truth spectra. To simulate low spatial-resolution HSIs, they down-sampled the images by a factor of 2 and to test the robustness of the architecture they add different levels of noise (SNR or signal-to-noise ratio).

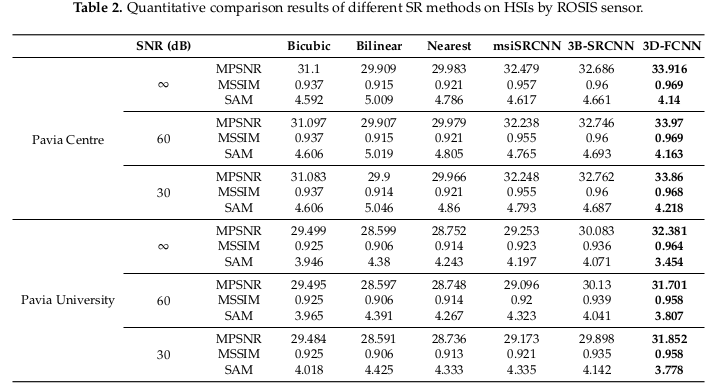
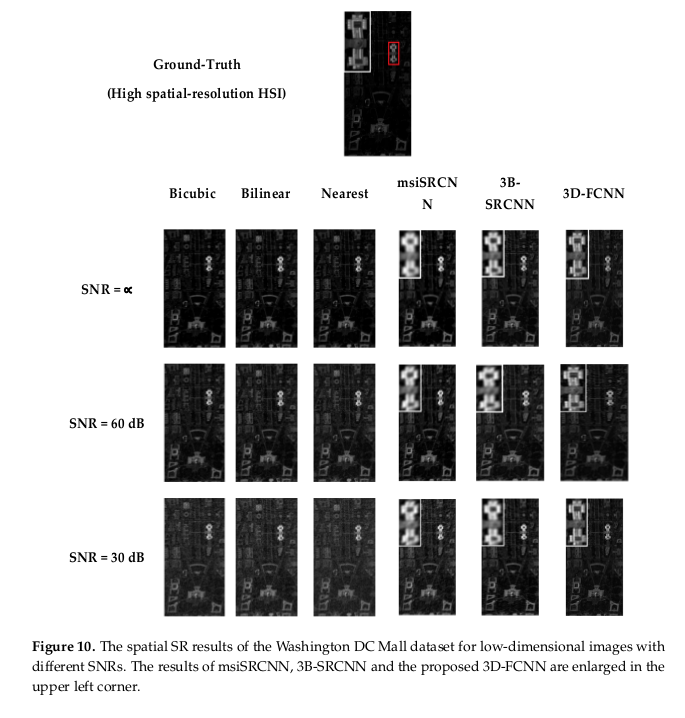
The results show a clear victory for the 3D-FCNN even with noise. The proposed 3D-FCNN based algorithm also achieves best spatial reconstruction for all the cases. The proposed 3D-FCNN based algorithm provides much better spectral fidelity no matter the dataset.

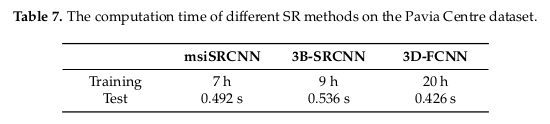
But those results have a cost, on an NVIDIA GTX1070 with 16GB memory, that takes 20h to train the model with 150 samples.