The authors propose an unsupervised method to discover transformation matrices to describe a dataset. To do so, the method looks at the closest neighbor of some samples and optimizes a novel convex problem.

Problem

Given an input \(x \in \Re^d\) we want a matrix \(A^{d \times d} such that, tAx + x = \bar x\), where \(t\) is a scaling factor and \(\bar x\) is the nearest neighbor.

We want to minimize the following equation :

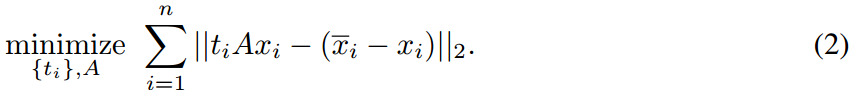
Learning transformations

The authors use Lie groups to define every transformation. A Lie group is a group for which the multiplication (\(\Re^d \rightarrow \Re^d\)) and the inversion are differentiable.

We want to minimize a weighted sum of vectors which would approximate the real transformation. The weights are noted as \(\alpha\)

We find for \(r >= d , A = \sum^{r}_{i=1}\alpha_{i}(\bar x_{i} - x_{i})x_{i}^{T}\)

For \(K\) transformation, we get for \(r > K^2 , A_k = \sum^{r}_{i=1}\alpha_{ik}(\bar x_{i} - x_{i})x_{i}^{T}\)

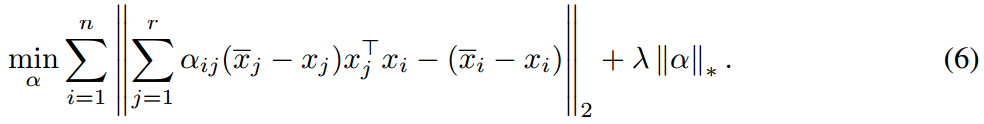
Disentangling Transformations

From a set of transformations \(A_{1..K}\) we want to extract uncorrelated transformations. We can find those by computing the SVD of those transformations. (See Theorem 3.4)

Experiments

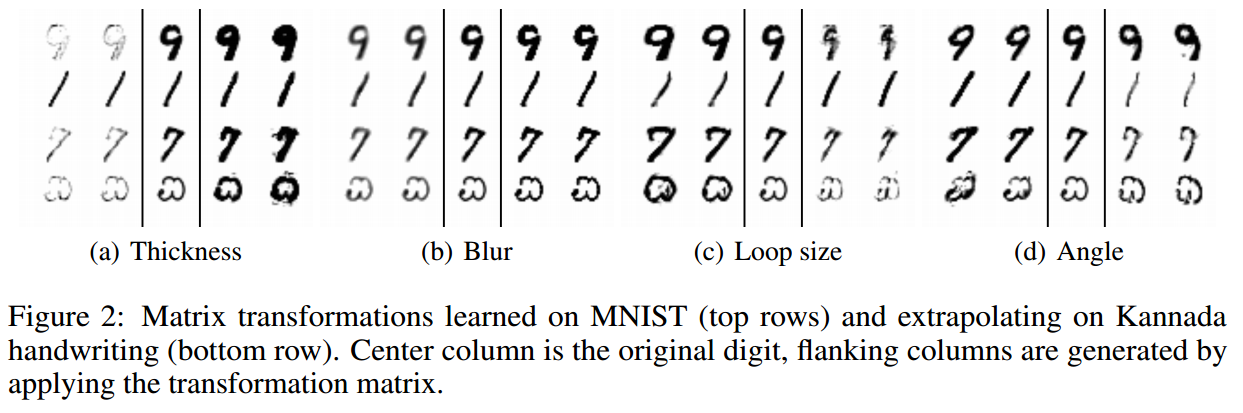
It took 10 minutes to find the most important transformations on MNIST. The authors also tried on another dataset (Kannada handwriting) without retraining. They also tested their method on CelebA (not shown here).

Here are some quantitative results.

Note : The Convex method is where they do not add a trace regularization and they do not use gradient descent.