Summary

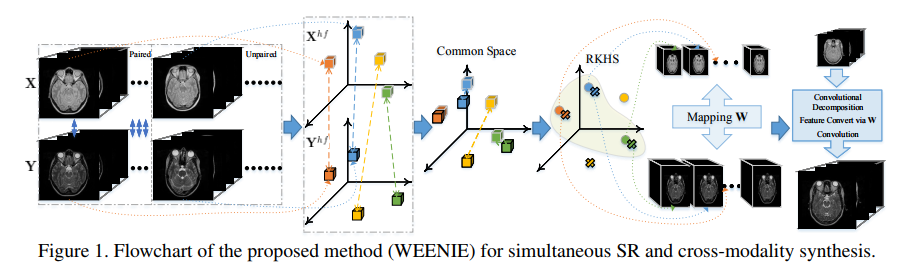
Acquisition of high-resolution, multimodal MRI images is long and costly. The authors propose a model to do both super-resolution and cross-modality image synthesis from low resolution images. Their method is called WEENIE (WEakly-supErvised joiNt convolutIonal sparsE coding).

More precisely, the goal is to be able to reconstruct a high resolution image from a low resolution image of different modality using Convolutional Sparse Coding (CSC).

The objective of CSC is to learn \(K\) filters \(\mathbf f_k\) and associated sparse feature maps \(\mathbf z_k\) such that the input \(\mathbf x\) can be reconstructed from the sum of the convolution of each pair of filter and sparse feature map. A constraint is added on the filters to make sure one filter does not absorb all the energy of the system.

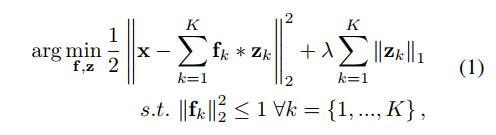
Learning the filters and sparse feature maps is done by minimizing both a reconstruction error and an \(l_1\) regularization on the feature maps. Furthermore, a mapping will also be learned to enforce that the LR feature maps are mappable to the HR feature maps.

Hetero-domain image alignment

The dataset is comprised of a small number of paired images (LR and HR MRI images of the same subject across dfferent modalities), and a high number of unpaired images (LR and HR MRI images are from different subjects and modalities).

Using paired data, an alignement between LR and HR images is learned using manually extracted high-frequency (HF) features (edges for the low-resolution images and textures for HR images). The alignment is then used to find new pairs in the unpaired images and augment the dataset.

Optimization

Here is the full objective function to jointly learn the filters, sparse feature maps and mapping function:

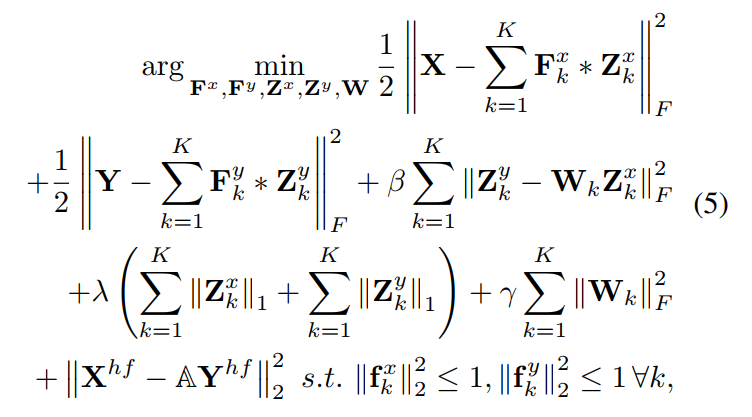
In practice however, the parameters cannot be learned jointly. Thus, optimization is done in 3 steps, where a single set of variables is optimized at each step.

  1. The sparse feature maps \(\mathbf Z^x\) and \(\mathbf Z^y\) are optimized using ADMM in the Fourier domain. In simple terms, the feature maps should be able to reconstruct the image when convoluted with the filters \(\mathbf F^x\) and \(\mathbf F^y\), \(\mathbf Z^x\) should be mappable to \(\mathbf Z^y\) using a mapping \(W\), and finally, they should be sparse.

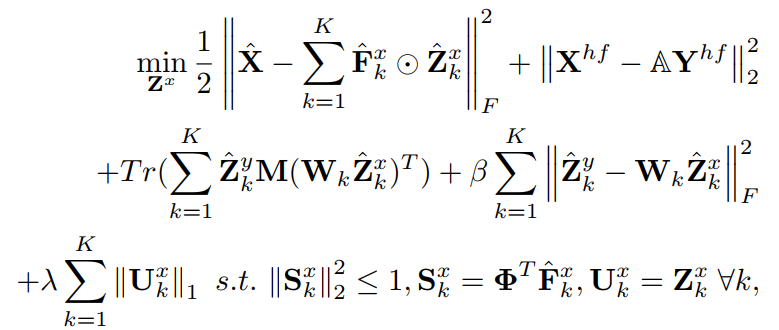
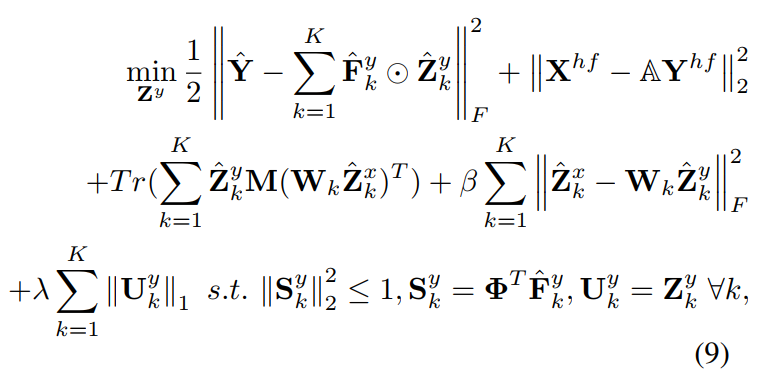
  1. The filters \(\mathbf F^x\) and \(\mathbf F^y\) are learned using least squares reconstruction.

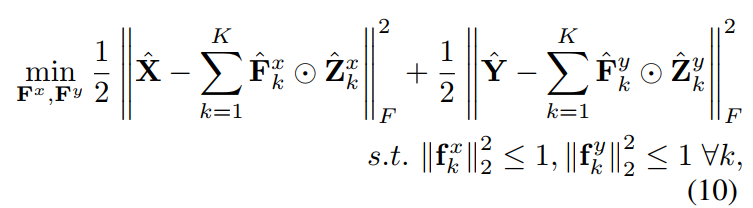
  1. The mapping function is learned using ridge regression with regularization such that the solution is analitically derived.

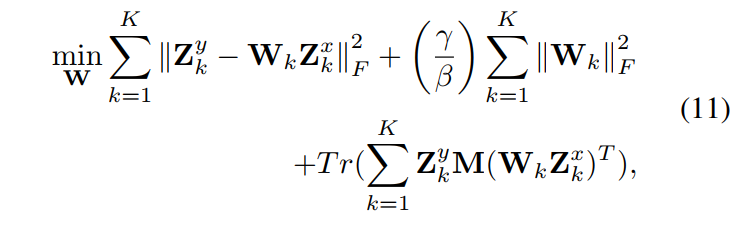
Those three optimization steps are repeated until convergence.

Once the training stage is complete, we are left with the learned filters (\(\mathbf F^x\) and \(\mathbf F^y\)) and mapping function (\(W\)).

Then, a HR test target image \(\mathbf Y^t\) can be reconstructed from a LR image \(\mathbf X^t\) of a different modality by computing the sparse feature maps \(\mathbf Z^t\) of \(\mathbf X^t\) with respect to the filters \(\mathbf F^x\), and then using the mapping function \(\mathbf W\) to map into the HR feature space, i.e. \(\hat \mathbf Z^t \approx \mathbf W \ast \mathbf Z^t\). Finally, \(Y^t\) is reconstructed by computing the sum of the K convoluted feature maps and filters. In summary:

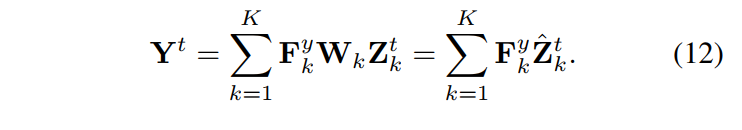
Experiments and Results

Datasets:

  • IXI: 278 x (256 x 256 x n)
  • NAMIC: 20 x (128 x 128 x m)

LR images are computed by downsampling HR ground truth images.

800 filters are learned, which the authors note is a good balance between computation complexity and result quality.

Baselines:

  • ScSR: Sparse coding SR
  • ANR: Anchored neighborhood regression
  • NE+LLE: Neighbor embedding + locally linear embedding
  • Zeyde’s method: local “Sparse-Land” model on image patches
  • CSC-SR: Convolutional sparse coding-based SR
  • A+: Adjusted anchored neighborhood regression

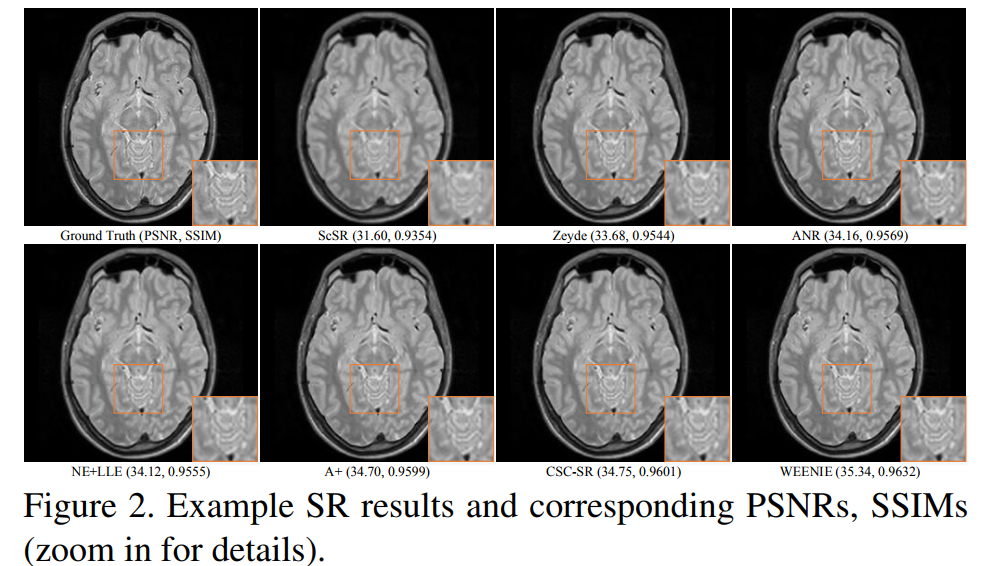
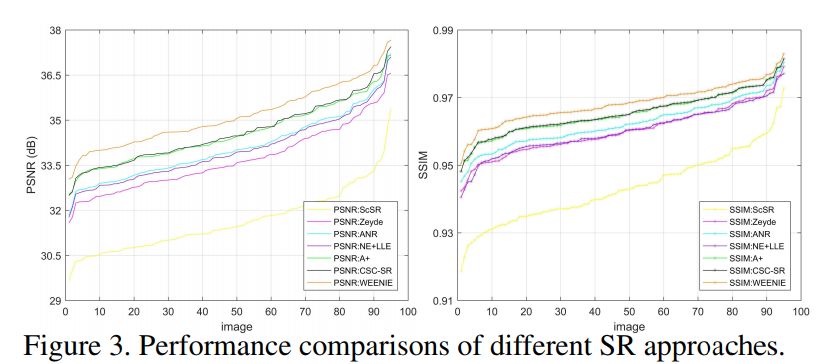
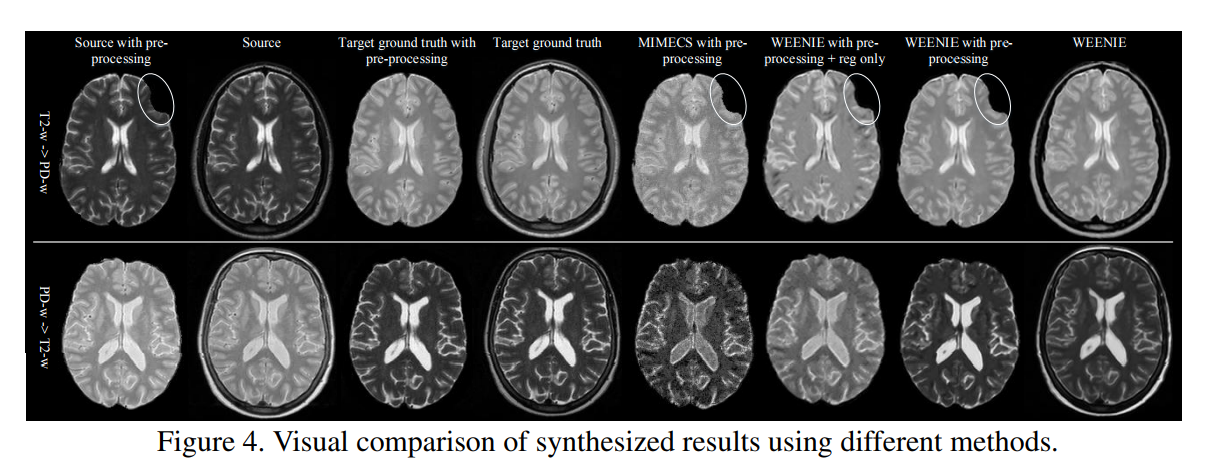
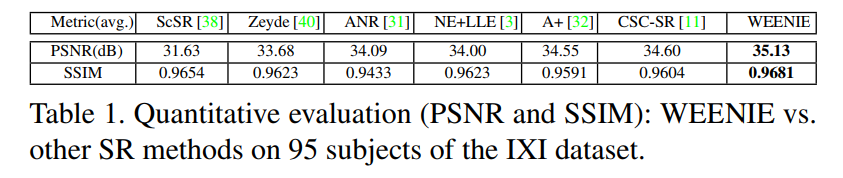
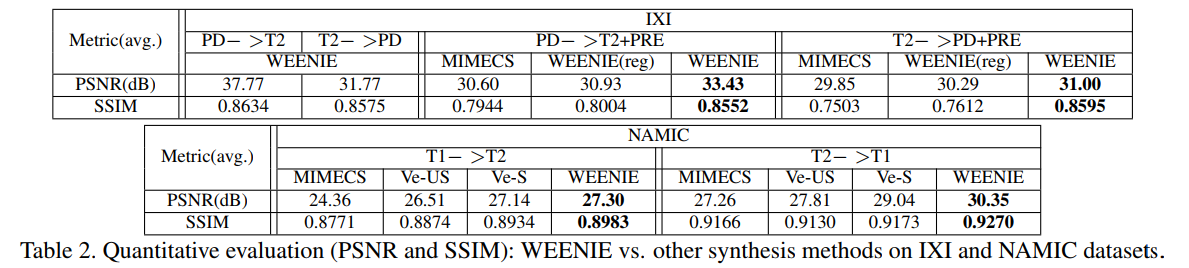
Results: