Summary

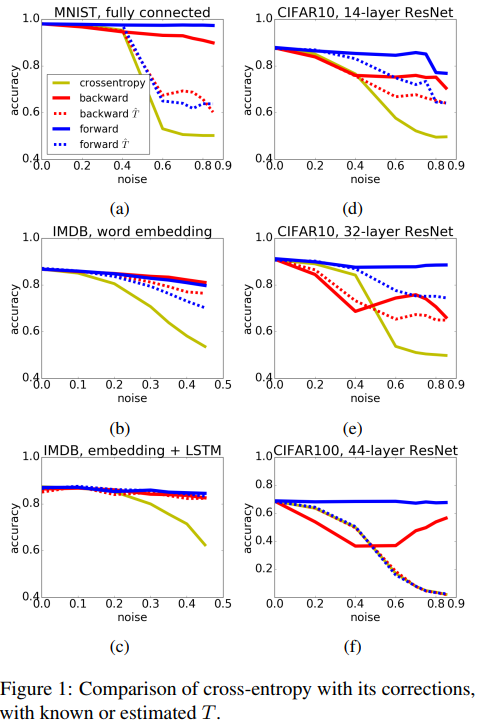
This paper proposes two procedures for loss correction in case of noisy labels that are agnostic to both application domain and network architecture. Their method simply amounts to at most a matrix inversion or a matrix multiplication

They suppose that the joint distribution of noisy labels data is modeled as

\[p(\vec x,\hat y) = \sum_y p(\hat y|y) p(y|\vec x)p(\vec x)\]

where

\[p(\hat y|y) = T \in [0, 1]^{c*c}\]

is the noise transition matrix specifying the probability of one label being flipped to another, i.e.:

\[\forall i, j, T_{ij} = p(\hat y = e^j |y = e^i).\]

In order to compensate for the noise, they propose 2 solutions : a forward correction procedure and a backward correction procedure. The forward correction amounts to multiply the output of the network with T

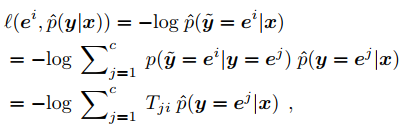
The backward correction amounts to multiply the loss by the inverse of T

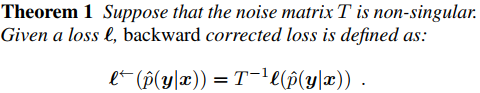
The algorithm to compute T is very simple and amounts to

Summary

You know what, it works!