Oriented Response Networks
Model
This papers provides a new way to use convolutions. In conventional convolutional neural networks, the filters are only invariant to translation, but the authors propose a new technique to also make them invariant to rotations. This method is called Oriented Response Network (ORN). The ORN is built on top of Active Rotating Filters (ARF).
ARF
An ARF \(\mathcal{F}\) is a filter of size \(W \times W \times N\) where \(N\) is the number of rotations during the convolution. These produce a feature map of \(N-1\) orientations. The rotated variant of \(\mathcal{F}\) called \(\mathcal{F}_\theta\) are constructed in two steps: coordinate rotation, and orientation spin.
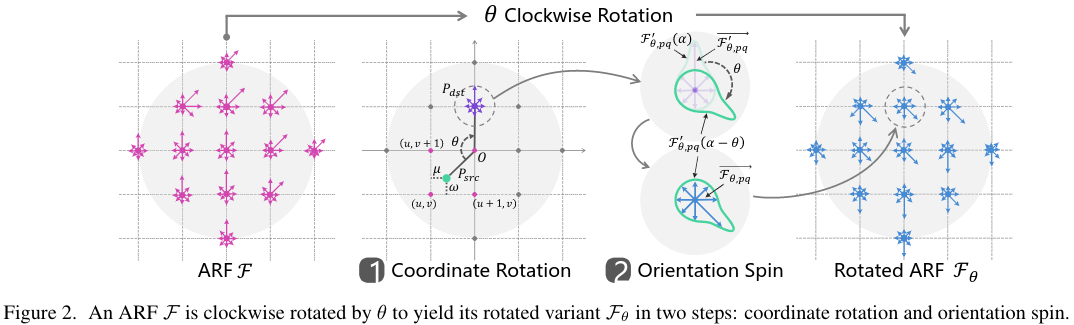
To be efficient, the coordinate rotation and orientation spin are calculated by the circular shift operator in the fourier domain.
Oriented Response Convolution (ORConv)
The ORConv can be seen as a composition of the ARF \(\mathcal{F}\) and an N-channel input feature map \(\mathcal{M}\). This combination is denoted as \(\hat\mathcal{M} = \mathbf{ORConv}(\mathcal{F}, \mathcal{M})\), where \(\hat\mathcal{M}\) are the output feature maps with \(\mathcal{N}\) orientations.
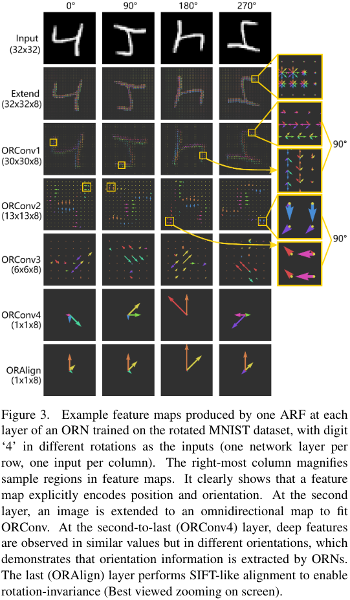
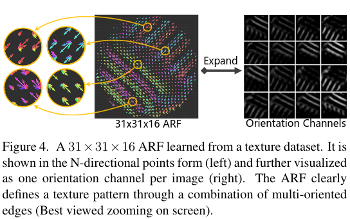
Rotation invariant Feature encoding
By default, the feature maps of ORN are not rotation invariant. When the task needs to be within-class rotation invariant they use two strategies, ORAlign and ORPooling.
Notation: \(\hat\mathcal{M}\{i\}^{(d)}\) where \(i\) is the i-th feature map of the ORConv layer, and \(d\) is the orientation.
ORAlign
The ORAlign simply computes the dominant orientation \(\mathcal{D} = \text{argmax}_d \hat\mathcal{M}\{i\}^{(d)}\) and rotate the feature by \(-\mathcal{D}\frac{2\pi}{N}\).
ORPooling
This pooling consists of simply extracting the maximum orientation of a given feature map \(\text{max}(\hat\mathcal{M}\{i\}^{(d)})\)
Results
They built an MNIST dataset with rotation from \([-\frac{\pi}{2}, \frac{\pi}{2}]\). They report results and show the feature encoding using tSNE for numbers that are similar, like \(6\) and \(9\).
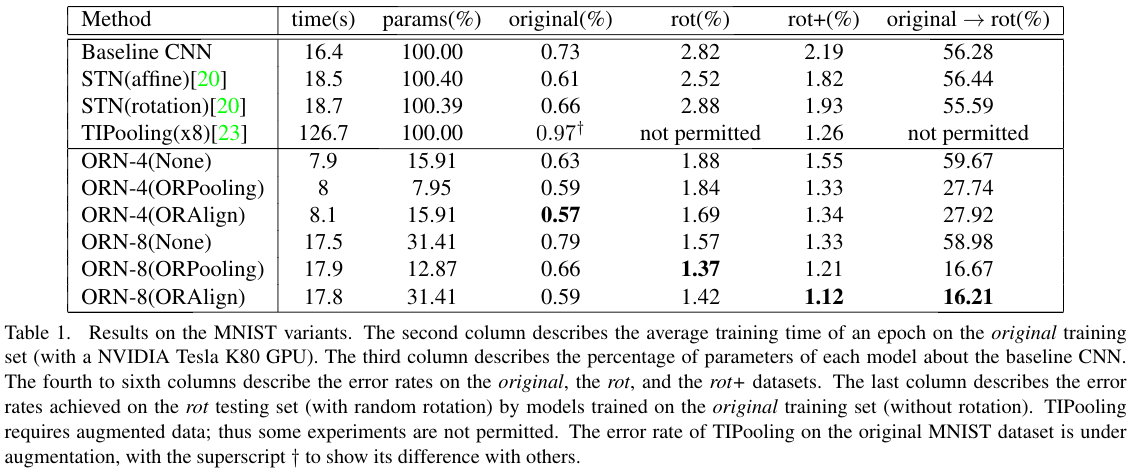
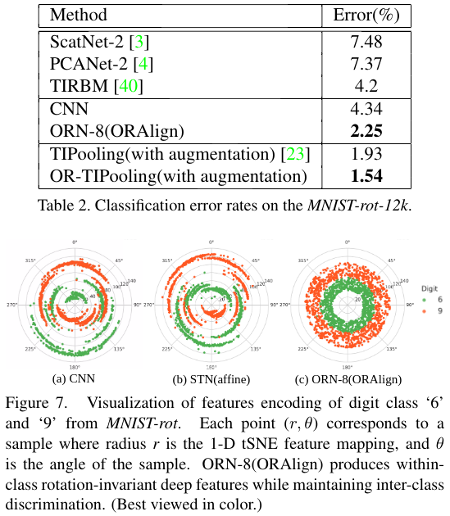
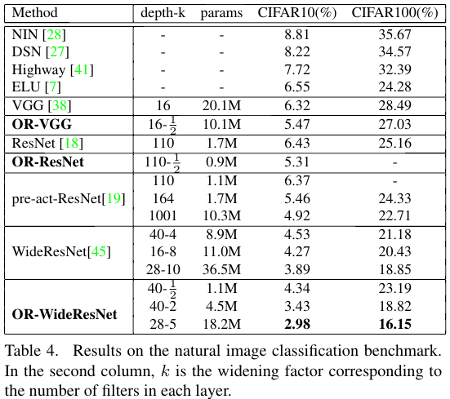
They also report results on CIFAR10 dataset and produce better results with less parameters.