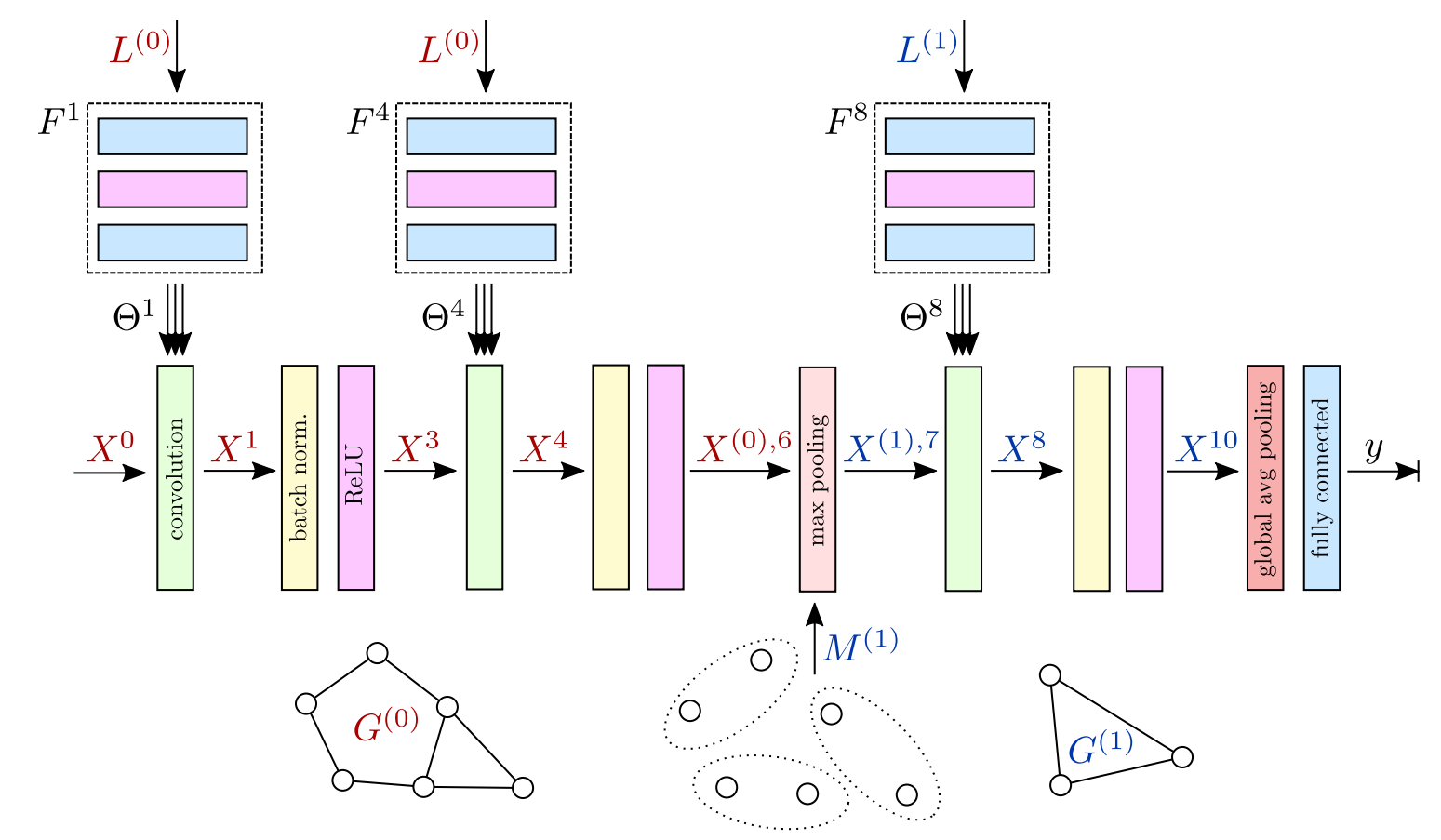
In this paper, the authors perform point cloud classification (like image classification) on graph whose configuration is not fixed. A graph whose configuration is not fixed is one for which the vertices do not have the same number of edges. The graph is constructed from a point cloud (typically obtained with a lidar scanner) and a pre-processing remeshing operation.

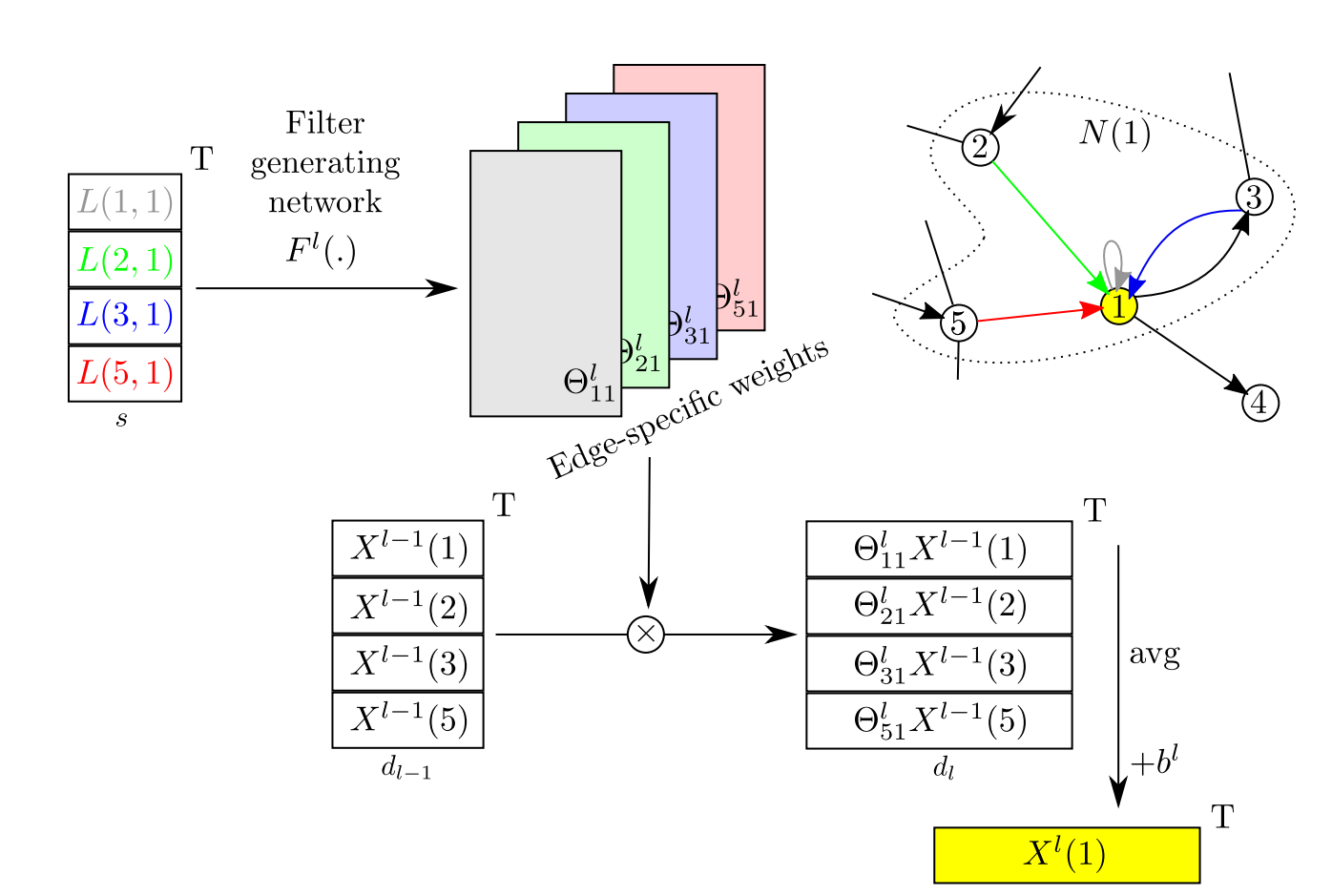
Since the number of edges is not the same for each vertices (unlike an image for example) they propose a new type of convolution operator which involves a function \(F\) which converts an edge label \(L\) and the weight vector \(w\) to a floating point value \(\Theta\). Note that in Fig.2, the use of \(F(L,w)\) allows to obtain a normal convolution (second equation). Note that \(X\) are feature maps, \(l\) is the layer index, \(w^l\) is the weight vector of layer \(l\), and \(b^l\) is the bias of layer \(l\).

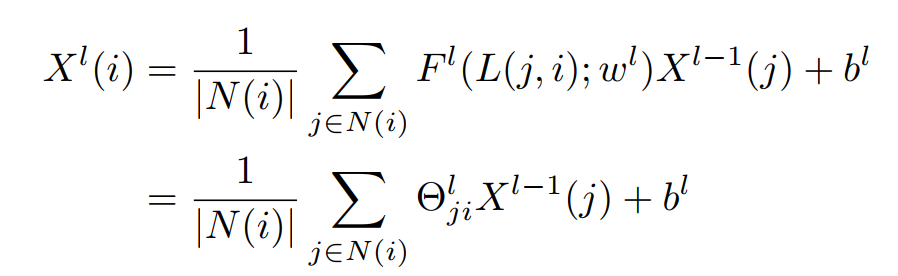
The overall graph-CNN has the same structure than a conventional CNN except for the MaxPooling operation which involves a graph reduction algorithm (\(M^{(1)}\) in the next figure).