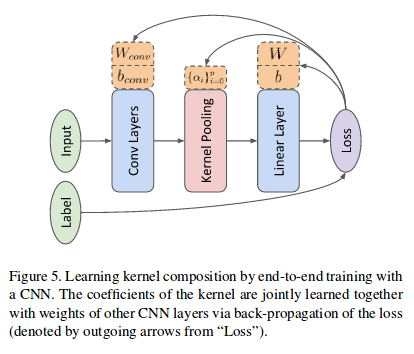
Kernel pooling for Convolutional Neural Network
Idea
‘Feature pooling’ means encoding and aggregating feature maps to obtain higher-order and non linear feature interactions between features (ex : add \(x_1x_2\) to \([x_1, x_2]\) as a new feature), and ‘kernel pooling’ implies to learn from the data which feature kernels would be best by using a differentiable approximated representation to learn the kernels’ parameters. It could be seen as an additional layer between convolutions (feature extraction) and linear layers (decision).
Method
Learn parameters of Taylor series kernels approximating gaussian RBF kernels
The p-level tensor product is the pth order polynomial kernel and the Taylor series kernel is the sum of the polynomial kernel multiplied by factors from 1 up to p. Its standard form is hardly applicable due to memory limitations => compact form with Count Sketch kernel approximation (TensorSketch): unbiased approximation
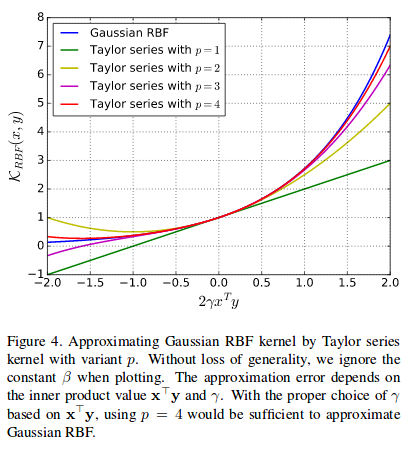
p=4 is enough to approximate a gaussian kernel and other decomposable kernels could be approximated (especially by learning coefficients)
Application
Tested on : ImageNet / CUB-200 / Stanford car set / FGComp2013 / Food101 with : VGG-16 / ResNet-50 When compared to bilinear pooling and state-of-the-art, this shows an improvement of about 1-3% with both architectures
With VGG, 2nd and 3rd order feature interactions were weighted a lot more than with ResNet, which possibly shows that there is a better intrinsic capture information with ResNet large receptive field and residual modules.
Approximating gaussian kernels :
Architecture to learn kernels :