Kernel density estimation (KDE) is a typical non-parametric estimation method, which assumes that the data do not follow a specific distribution. That is a key difference between KDE and other Gaussian mixture models(GMM) based methods.

KDE tried to estimate the distribution of each pixel in a video with the formula: ,

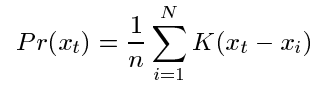where x_i is the pixel value at time i, N is the total number of pixels in the sample, and K is the kernel function (normal distribution) with its sigma equal to: ,

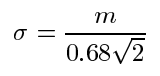where m is the median of x_i-x_{i+1} in the sample.

KDE supposes to have a quicker reaction to changes comparing with GMM. The speed reported by the paper is “15-20 frame per second on a 400 MHz pentium processor for 320x240 gray scale images” at 2000.