Layer Normalization is a simple method used to reduce training time in deep neural networks. It can also stabilize the hidden state dynamics in recurrent networks. It is similar to Batch Normalization, but is not dependent on mini-batch size, and performs the same computation at training and testing time.

How it works

Layer normalization works by computing the normalization statistics (mean and variance) from all of the summed inputs to the neurons within a hidden layer (on a single training case).

Notation

We consider the \(l^{th}\) hidden layer of a feed-forward neural network. The input vector to each hidden unit is noted as \(h^l\), while the output of the \(i^{th}\) unit is noted as \(h_i^{l+1}\) and is computed as such:

\[a_i^l = {w_i^l}^{\top} h^l \qquad \qquad h_i^{l+1} = f(a_i^l + b_i^l)\]

where \(a_i^l\) is the summed inputs to the unit, \(f(\cdot)\) is an element-wise non-linear function, \(w_i^l\) is the weight vector and \(b_i^l\) is the scalar bias parameter.

Batch normalization

Batch normalization was introduced to reduce “covarate shift”. It normalizes the summed inputs to each hidden unit over the training cases. Specifically, for the \(i^{th}\) summed input in the \(l^{th}\) layer, the batch normalization method rescales the summed inputs according to their variances under the distribution of the data.

\[\bar{a}_i^l = \frac{g_i^l}{\sigma_i^l} (a_i^l - \mu_i^l) \qquad \mu_i^l = \mathop{\mathbb{E}}\limits_{\mathbf{x} \sim P(\mathbf{x})} [a_i^l] \qquad \sigma_i^l = \sqrt{\mathop{\mathbb{E}}\limits_{\mathbf{x} \sim P(\mathbf{x})} [(a_i^l - \mu_i^l)^2]}\]

where \(\bar{a}_i^l\) is the normalized summed inputs to the \(i^{th}\) hidden unit in the \(l^{th}\) layer, and \(g_i\) is a gain parameter scaling the normalized activation before the non-linear activation function.

Layer normalization

Instead of normalizing over the data distribution, this method suggests to compute the normalization statistics over all the hidden units in the same layer:

\[\mu^l = \frac{1}{H} \sum\limits_{i=1}^H a_i^l \qquad \sigma^l = \sqrt{\frac{1}{H} \sum\limits_{i=1}^H (a_i^l - \mu^l)^2}\]

where \(H\) is the number of hidden units in the layer.

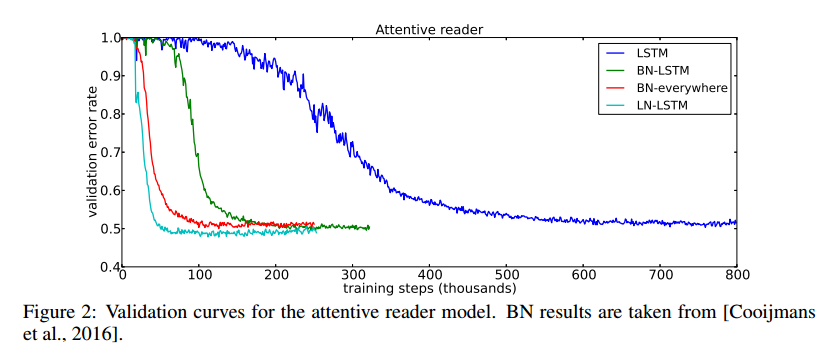
Here are the results of a unidirectional attentive reader model trained on the CNN corpus question-answering task:

Limitations

Speed: While layer normalization will speed up training in terms of the number of epochs/updates, it will also slow down training in terms of time per epoch/update, because moment computation is much slower on GPU compared to simple matrix multiplications. Overall, it should still usually speed up global training time, and hopefully give better results, but there is no guarantee.

CNNs: “In our preliminary experiments, we observed that layer normalization offers a speedup over the baseline model without normalization, but batch normalization outperforms the other methods. […] We think further research is needed to make layer normalization work well in ConvNets.”