Xception: Deep Learning with Depthwise Separable Convolutions

Xception is a model which improves upon the Inception V3 model¹.

What is a Depthwise Separable Convolution

A depthwise separable convolution, commonly called “separable convolution” in deep learning frameworks such as TensorFlow and Keras, consists in a sequence of two operations:

1. A depthwise convolution, i.e. a spatial convolution performed independently over each channel of an input, and
2. a pointwise convolution, i.e. a 1x1 convolution, projecting the channels output by the depthwise convolution onto a new channel space.

This is not to be confused with a spatially separable convolution, which is also commonly called “separable convolution” in the image processing community.

Why Separable Convolutions ?

The author postulates that “the fundamental hypothesis behind Inception is that cross-channel correlations and spatial correlations are sufficiently decoupled that it is preferable not to map them jointly”. This decoupling is implemented in the Inception module by a 1x1 convolution followed by a 3x3 convolution (see fig. 1 and 2).

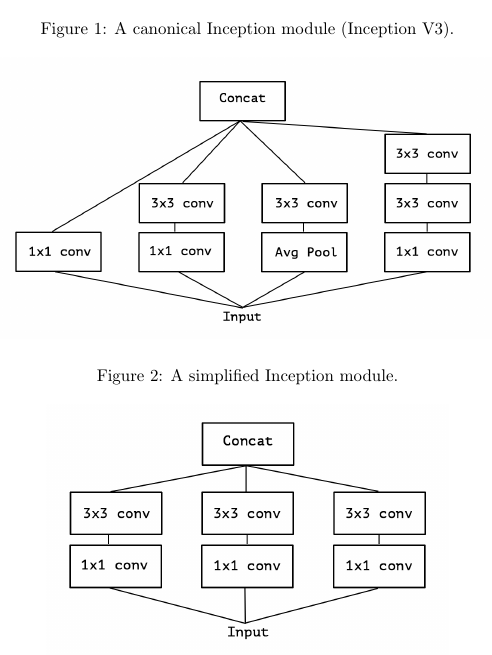
Furthermore, the author makes the following proposition : the Inception module lies in a discrete spectrum of formulations. At one extreme of this spectrum we find the regular convolution, which spans the entire channel space (there is a single segment). The reformulation of the simplified Inception module in figure 3 uses three segments. Figure 4 shows a module that uses a separate convolution for each channel, which is almost a depthwise separable convolution (more on this below).

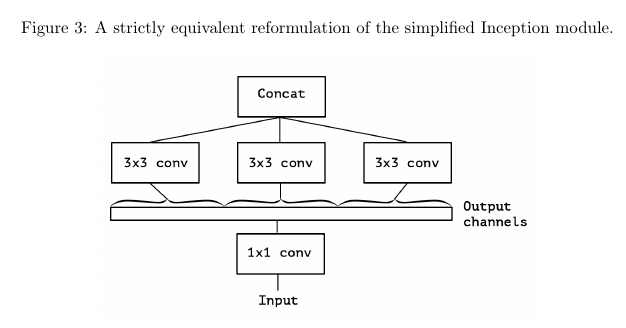
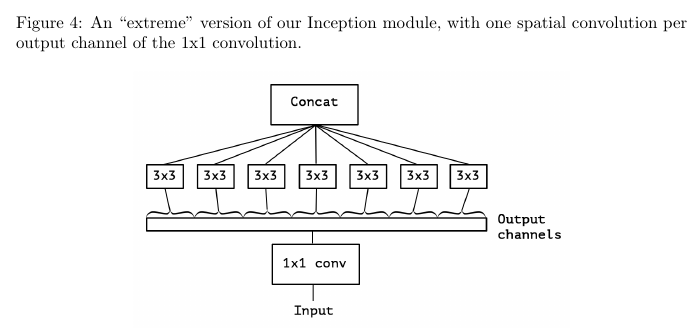
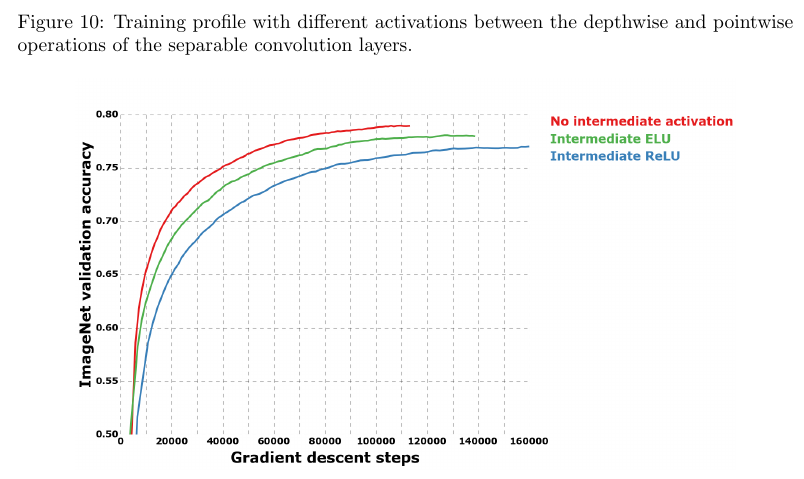
There is two minor differences between a depthwise separable convolution and the module shown in figure 4 : (1) the order of the two operations, and (2) the presence or absence of a non-linearity between those operations. The author argues that the first does not matter. The second difference is important, and the absence of non-linearity improves accuracy (see figure 10). An opposite result is reported by Szegedy et al. for Inception modules. Chollet provides an explanation in section 4.7.

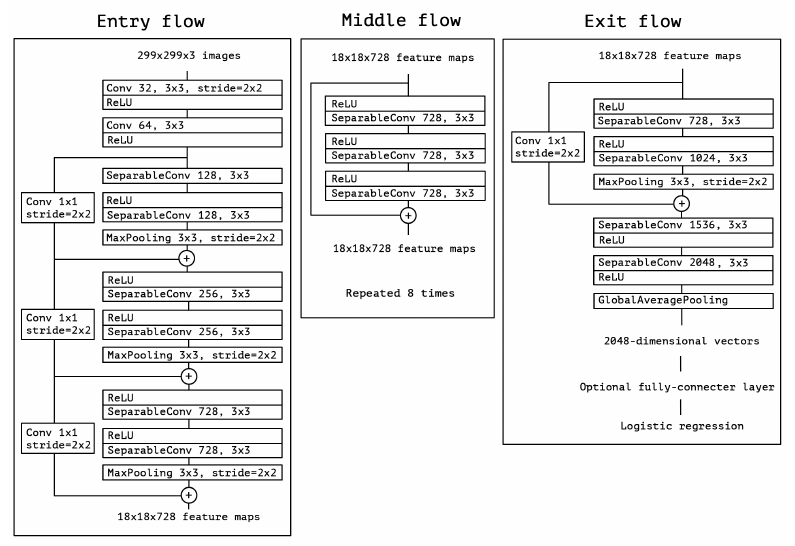
The Xception Architecture

In short, the Xception architecture is a linear stack of depthwise separable convolution layers with residual connections. “Xception” means “Extreme Inception”, as this new model uses depthwise separable convolutions, which are at one extreme of the spectrum described above.

Experimental evaluation

Two datasets were used : ImageNet (1000 classes) and JFT, an internal Google dataset comprising 350 million high-res images with labels from a set of 17,000 classes. For each dataset, an Inception V3 model and an Xception model were trained. Models trained on JFT were evaluated using a smaller auxiliary dataset, named FastEval14k. The networks were trained on 60 NVIDIA K80 GPUs each². The ImageNet experiments took 3 days each, while the JFT experiments took over one month each. Note the great amount of resources invested, both in terms of money and time.

On ImageNet, Xception shows marginally better results than Inception V3. On JFT, Xception shows a 4.3% relative improvement on the FastEval14k MAP@100 metric (see table 1). The fact that both architectures have almost the same number of parameters indicates that the improvement seen on ImageNet and JFT does not come from added capacity but rather from a more efficient use of the model parameters. The author also point out that Xception outperforms ImageNet results reported by He et al. for ResNet-50, ResNet-101 and ResNet-152.

Table 1: Classification performance comparison on JFT (single crop, single model). The models with FC layers have two 4096-unit FC layers before the logistic regression layer at the top. MAP@100 is the mean average precision on the top 100 guesses.

Model	JFT FastEval14k MAP@100
Inception V3 - no FC layers	6.36
Inception V3 - with FC layers	6.50
Xception - no FC layers	6.70
Xception - with FC layers	6.78

Future directions

The author says that there is no reason to believe that depthwise separable convolutions are optimal. It may be that intermediate points on the spectrum, lying between regular Inception modules and depthwise separable convolutions, hold further advantages.

---